The Geometric Conundrum: Is A Square A Trapezoid?

Is a square a trapezoid? This question might appear straightforward at first glance, yet it opens up a fascinating world of geometrical exploration and debate. Geometry, the study of shapes, sizes, and properties of space, often presents seemingly simple questions that challenge our understanding of conventional definitions. The inquiry into whether a square qualifies as a trapezoid is one such captivating subject that invites both students and enthusiasts alike to delve deeper into the intricacies of geometric classification. In this article, we will navigate through the definitions, properties, and characteristics of these shapes to determine the relationship between them.

At the heart of this exploration lies the fundamental question of how we define and categorize shapes. A square, with its equal sides and angles, possesses a unique set of properties that distinguish it from other quadrilaterals. Meanwhile, a trapezoid, often characterized by having only one pair of parallel sides, has its own distinctive traits. The challenge arises when we attempt to reconcile these definitions and determine whether a square can fit within the broader classification of a trapezoid. The journey to answer this question not only enhances our understanding of geometry but also encourages us to think critically about how definitions shape our perception of mathematical concepts.

Before we dive into the debate, it is essential to approach this topic with an open mind. Geometry is not just about rigid definitions but also about understanding the relationships between different shapes and their properties. By examining the characteristics of both squares and trapezoids, we can uncover the underlying principles that govern their classification. This exploration will not only help us answer the question "is a square a trapezoid?" but also enrich our appreciation for the beauty and complexity of geometric shapes.

Understanding Quadrilaterals
Defining a Square
Properties of a Square
Defining a Trapezoid
Properties of a Trapezoid
The Square as a Special Trapezoid
Geometric Theorems and Square-Trapezoid Relation
Historical Perspectives on Geometric Definitions
Educational Implications of Geometric Classifications
Real-World Applications of Shape Classification
Common Misconceptions in Geometry
Visualizing Geometric Shapes
Advanced Geometric Concepts Related to Squares and Trapezoids
Conclusion
Frequently Asked Questions

Understanding Quadrilaterals

Quadrilaterals are four-sided polygons that form the foundation of many geometric concepts. Understanding these shapes is crucial to delving into the specifics of squares and trapezoids. Quadrilaterals can be classified into various categories based on their sides and angles, such as squares, rectangles, parallelograms, rhombuses, and trapezoids. Each of these categories has its own set of defining properties that help distinguish one quadrilateral from another.

The general properties of quadrilaterals include having four sides, four vertices, and the sum of their interior angles totaling 360 degrees. However, the specific characteristics of each type of quadrilateral can vary significantly. For example, a rectangle has opposite sides that are equal and angles that are all right angles, while a rhombus has all sides of equal length but does not necessarily have right angles.

The classification of quadrilaterals is based on their unique properties, which can include parallel sides, equal angles, and congruent diagonals. This classification system allows us to understand and identify the relationships between different quadrilaterals and explore how they relate to one another in a geometric context, setting the stage for our examination of squares and trapezoids.

Defining a Square

A square is a specific type of quadrilateral that is both a rectangle and a rhombus. It is defined by its equal sides and angles, making it a regular polygon. A square has four sides of equal length and four right angles, each measuring 90 degrees. This symmetry and regularity make the square a unique and easily recognizable shape within the realm of quadrilaterals.

One of the defining features of a square is its equal diagonals that bisect each other at right angles. The diagonals of a square are congruent, meaning they have the same length, and they intersect at the center of the square, creating four right-angled isosceles triangles. This property of equal diagonals is shared with rectangles, further highlighting the square's classification as a type of rectangle.

In addition to its geometric properties, a square also holds significance in various mathematical contexts. It serves as a fundamental unit of measurement in geometry, often representing the base unit for area calculations. The square's area is calculated by squaring the length of one of its sides, emphasizing its role as a building block for understanding more complex geometric shapes.

Properties of a Square

The properties of a square are distinct and serve as the basis for its classification as a unique quadrilateral. Understanding these properties is essential for examining how a square relates to other quadrilaterals, including trapezoids. Here are some key properties of a square:

Equal Sides: A square has four sides of equal length. This property sets it apart from rectangles, which have pairs of equal sides, and from other quadrilaterals with varying side lengths.
Right Angles: All four angles in a square are right angles, each measuring 90 degrees. This uniformity in angles is a defining characteristic of squares and rectangles.
Congruent Diagonals: The diagonals of a square are equal in length and bisect each other at right angles. This property is shared with rectangles and is crucial for understanding the symmetry of the square.
Regular Polygon: A square is a regular polygon, meaning it has equal sides and equal angles. This regularity is what distinguishes it from other quadrilaterals with varying side lengths and angles.
Symmetrical: A square is symmetrical along both its diagonals and its horizontal and vertical axes. This symmetry contributes to its aesthetic appeal and mathematical significance.

These properties collectively define a square and set the stage for examining its relationship with trapezoids, which we will explore in subsequent sections.

Defining a Trapezoid

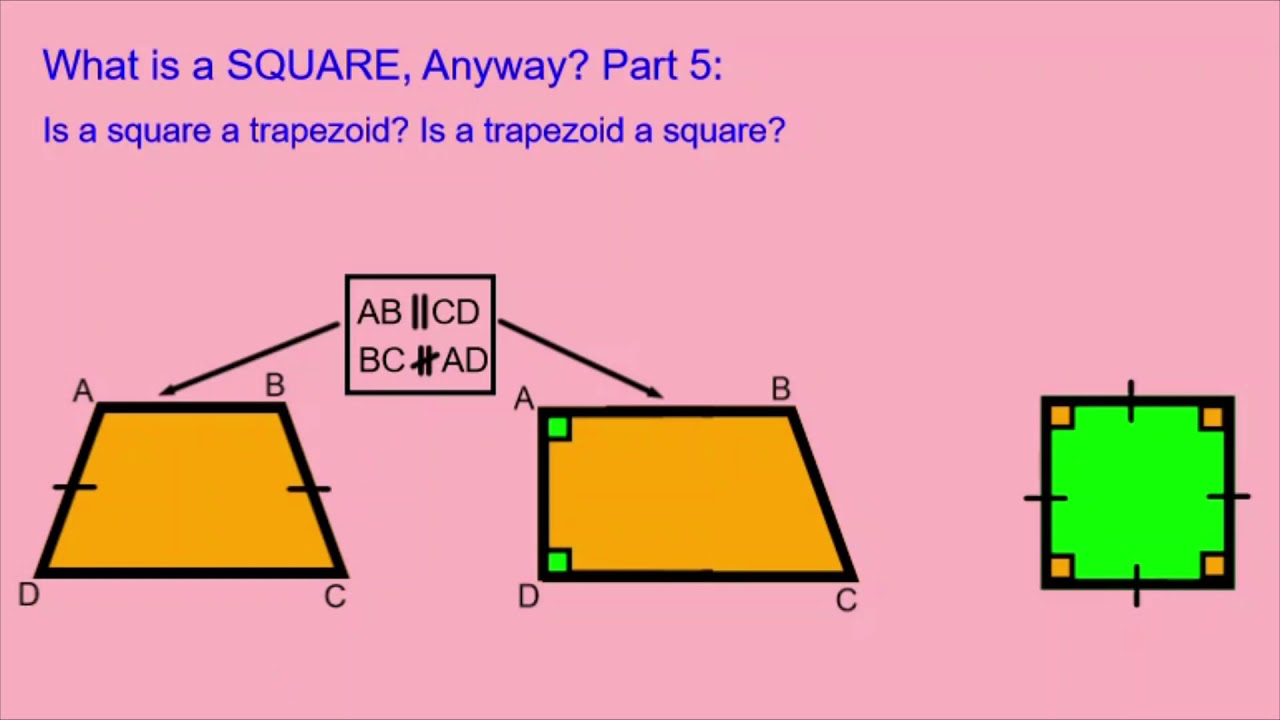
A trapezoid, also known as a trapezium in some regions, is a quadrilateral with at least one pair of parallel sides. This definition distinguishes trapezoids from other quadrilaterals, such as squares and rectangles, which have two pairs of parallel sides. The parallel sides of a trapezoid are referred to as bases, while the non-parallel sides are called legs.

The defining characteristic of a trapezoid is its single pair of parallel sides, which creates a unique set of properties. The non-parallel sides can vary in length, and the angles formed by these sides with the bases can differ, resulting in trapezoids of various shapes and sizes. This flexibility in shape and form is what distinguishes trapezoids from more rigid quadrilaterals like squares and rectangles.

Trapezoids can be further classified into different types based on additional properties. An isosceles trapezoid, for example, has legs of equal length and equal base angles, resulting in a symmetrical shape. A right trapezoid has a right angle between one of its legs and a base, creating a distinct geometric form. These classifications help to understand the diversity of trapezoids and their relationship with other quadrilaterals.

Properties of a Trapezoid

The properties of a trapezoid are defined by its single pair of parallel sides and the angles formed by its non-parallel sides. These properties are essential for understanding the unique nature of trapezoids and how they relate to other quadrilaterals. Here are some key properties of a trapezoid:

Parallel Sides: A trapezoid has at least one pair of parallel sides, known as bases. This property is the defining characteristic of trapezoids and sets them apart from other quadrilaterals.
Non-Parallel Sides: The non-parallel sides, or legs, of a trapezoid can vary in length and angle, resulting in different shapes and forms.
Angle Variation: The angles formed by the non-parallel sides with the bases can vary, leading to diverse trapezoid shapes.
Classification Types: Trapezoids can be classified into isosceles, right, and scalene types based on additional properties, such as equal legs or right angles.
Area Calculation: The area of a trapezoid is calculated using the formula: (1/2) * (Base1 + Base2) * Height, where Base1 and Base2 are the lengths of the parallel sides, and Height is the perpendicular distance between the bases.

These properties define the essence of trapezoids and provide a framework for exploring their relationship with squares and other quadrilaterals.

The Square as a Special Trapezoid

The intriguing question of "is a square a trapezoid?" arises from the definitions and properties of these shapes. At first glance, the defining characteristic of a trapezoid—having at least one pair of parallel sides—might suggest that a square could qualify as a trapezoid, given that it has two pairs of parallel sides. However, this classification requires a deeper understanding of geometric definitions and relationships.

By definition, a square is a specific type of quadrilateral with equal sides and right angles. It is also a type of rectangle and rhombus due to its congruent sides and angles. A trapezoid, on the other hand, is defined by its single pair of parallel sides. While a square does have parallel sides, its unique properties, such as equal sides and right angles, set it apart from the more flexible definition of a trapezoid.

In some mathematical contexts, a square can be considered a special type of trapezoid. This is because a trapezoid is broadly defined as having at least one pair of parallel sides, and a square meets this criterion with its two pairs of parallel sides. However, this classification is not universally accepted, as it relies on a broader interpretation of trapezoids that includes shapes with additional properties like squares.

The question of whether a square is a trapezoid ultimately depends on the definitions and context in which these shapes are considered. While a square can be viewed as a special trapezoid in certain contexts, it is more commonly recognized as a distinct quadrilateral with its own set of defining properties.

Geometric Theorems and Square-Trapezoid Relation

Geometric theorems provide a framework for understanding the relationships between different shapes and their properties. These theorems can offer insights into the classification of squares and trapezoids and help determine whether a square can be considered a trapezoid.

One of the fundamental theorems related to quadrilaterals is the Parallel Line Theorem, which states that if a quadrilateral has at least one pair of parallel sides, it can be classified as a trapezoid. This theorem supports the idea that a square, with its two pairs of parallel sides, meets the basic criteria for being a trapezoid. However, the additional properties of a square, such as equal sides and right angles, complicate this classification.

Another relevant theorem is the Angle-Sum Theorem, which states that the sum of the interior angles of a quadrilateral is 360 degrees. This theorem applies to all quadrilaterals, including squares and trapezoids, and highlights the commonalities between these shapes. However, it does not provide a definitive answer to the question of whether a square is a trapezoid.

Geometric theorems can offer valuable insights into the relationships between different shapes, but they also illustrate the complexity of geometric classification. The question of whether a square is a trapezoid requires a nuanced understanding of these theorems and the specific properties that define each shape.

Historical Perspectives on Geometric Definitions

The history of geometry is rich with evolving definitions and classifications of shapes. Understanding the historical context of geometric concepts can provide insights into the question of whether a square is a trapezoid and how these shapes have been classified over time.

In ancient Greece, geometry was primarily concerned with the study of shapes and their properties. The Greek mathematician Euclid, often referred to as the "father of geometry," laid the foundation for geometric classification with his work "Elements." Euclid's definitions of shapes, including squares and trapezoids, were based on their properties and relationships, establishing the groundwork for modern geometric concepts.

Over time, the definitions and classifications of geometric shapes have evolved to accommodate new mathematical discoveries and insights. In the 19th and 20th centuries, the development of non-Euclidean geometry and the exploration of higher-dimensional spaces prompted mathematicians to reconsider traditional definitions and classifications of shapes.

Historical perspectives on geometric definitions highlight the dynamic nature of mathematical concepts and the importance of understanding the context in which these definitions were developed. The question of whether a square is a trapezoid reflects this ongoing evolution and the need to consider multiple perspectives in geometric classification.

Educational Implications of Geometric Classifications

The classification of geometric shapes has significant implications for education, particularly in the teaching of mathematics and geometry. Understanding the definitions and relationships between shapes, such as squares and trapezoids, is essential for developing a comprehensive understanding of geometric concepts.

In educational settings, the question of whether a square is a trapezoid can serve as a thought-provoking exercise that encourages students to think critically about geometric definitions and classifications. By exploring the properties of different shapes and their relationships, students can develop a deeper understanding of geometry and enhance their problem-solving skills.

Geometric classification also plays a crucial role in the development of mathematical reasoning and logical thinking. By examining the relationships between shapes and their properties, students can learn to apply deductive reasoning and develop a more nuanced understanding of mathematical concepts.

Incorporating questions like "is a square a trapezoid?" into educational curricula can foster an engaging and interactive learning environment that promotes critical thinking and exploration of geometric concepts. This approach can help students develop a strong foundation in geometry and prepare them for more advanced mathematical studies.

Real-World Applications of Shape Classification

The classification of geometric shapes has practical applications in various fields, including engineering, architecture, design, and computer graphics. Understanding the properties and relationships of shapes, such as squares and trapezoids, is essential for solving real-world problems and creating functional designs.

In engineering, the classification of shapes is crucial for designing structures and components that meet specific requirements. For example, the use of trapezoidal shapes in bridge design can provide stability and support, while the use of squares in grid patterns can ensure uniformity and balance.

In architecture, geometric classification informs the design of buildings and spaces, allowing architects to create aesthetically pleasing and structurally sound designs. The use of squares and trapezoids in architectural elements, such as windows and rooflines, can enhance the visual appeal and functionality of a structure.

In computer graphics, the classification of shapes is essential for creating realistic and visually appealing images and animations. Understanding the properties of squares and trapezoids can help graphic designers develop accurate representations of objects and environments.

The real-world applications of shape classification highlight the importance of understanding geometric concepts and their practical implications. By exploring the relationships between different shapes, such as squares and trapezoids, we can enhance our ability to solve complex problems and create innovative designs.

Common Misconceptions in Geometry

Geometry, like many areas of mathematics, is prone to misconceptions and misunderstandings. These misconceptions can arise from incomplete definitions, oversimplifications, or a lack of understanding of geometric principles. Addressing these misconceptions is essential for developing a clear and accurate understanding of geometric concepts.

One common misconception in geometry is the belief that all quadrilaterals with parallel sides are trapezoids. While trapezoids are defined by having at least one pair of parallel sides, other quadrilaterals, such as parallelograms and rectangles, also have parallel sides but are classified based on additional properties.

Another misconception is the assumption that all shapes with equal sides are squares. While squares do have equal sides, other quadrilaterals, such as rhombuses, also possess this property but differ in their angles and overall shape.

The question of whether a square is a trapezoid can also lead to misconceptions if not carefully examined. While a square does have parallel sides, its additional properties, such as equal angles and congruent diagonals, set it apart from the more general definition of a trapezoid.

Addressing these misconceptions requires a comprehensive understanding of geometric definitions and properties, as well as an exploration of the relationships between different shapes. By clarifying these concepts, we can promote a more accurate and nuanced understanding of geometry.

Visualizing Geometric Shapes

Visualization is a powerful tool for understanding geometric shapes and their properties. By creating mental images or using visual aids, we can better grasp the relationships between different shapes, such as squares and trapezoids, and their defining characteristics.

One way to visualize geometric shapes is through the use of diagrams and models. These visual aids can help illustrate the properties of shapes, such as parallel sides, equal angles, and congruent diagonals, and provide a clear representation of their relationships.

Interactive tools, such as computer software and online applications, can also enhance our ability to visualize geometric concepts. These tools allow us to manipulate shapes, explore their properties, and observe the effects of different transformations, such as rotations and reflections.

Visualization can also be enhanced through the use of physical models and hands-on activities. By constructing models of squares and trapezoids, we can develop a tactile understanding of their properties and relationships, reinforcing our comprehension of geometric concepts.

By incorporating visualization techniques into the study of geometry, we can enhance our understanding of shapes and their properties, making it easier to explore complex questions like "is a square a trapezoid?" and develop a deeper appreciation for the beauty and intricacy of geometric shapes.

As we delve deeper into the world of geometry, we encounter advanced concepts that build upon our understanding of basic shapes like squares and trapezoids. These concepts expand our knowledge of geometric relationships and provide new insights into the classification and properties of shapes.

One such concept is the idea of transformation, which involves changing the position, size, or orientation of a shape while retaining its basic properties. Transformations, such as translations, rotations, and reflections, can help us explore the relationships between squares and trapezoids and their transformations in the geometric plane.

Another advanced concept is the study of symmetry, which examines the balanced and proportional arrangement of shapes. Symmetry plays a crucial role in understanding the properties of squares, with their equal sides and angles, and trapezoids, with their parallel sides and varying angles.

Topology, a branch of mathematics that explores the properties of shapes that remain unchanged under continuous transformations, also offers insights into the classification of squares and trapezoids. Topological concepts can help us understand the fundamental characteristics of shapes and their relationships, regardless of their specific geometric properties.

By exploring these advanced geometric concepts, we can deepen our understanding of squares and trapezoids, their properties, and their classification. This exploration enhances our appreciation for the complexity and beauty of geometry and provides new perspectives on questions like "is a square a trapezoid?"

Conclusion

The question "is a square a trapezoid?" invites us to explore the intricate world of geometric classification and the relationships between different shapes. Through our examination of the definitions, properties, and characteristics of squares and trapezoids, we have uncovered the complexity and nuance of geometric concepts.

A square, with its equal sides and right angles, is a unique and distinct quadrilateral that possesses a set of defining properties. While it shares some characteristics with trapezoids, such as parallel sides, its unique features, such as congruent diagonals and symmetry, set it apart from the broader definition of a trapezoid.

Ultimately, the classification of a square as a trapezoid depends on the context and definitions used in geometric exploration. In some contexts, a square can be considered a special type of trapezoid due to its parallel sides. However, it is more commonly recognized as a distinct shape within the realm of quadrilaterals.

Our exploration of this question has not only expanded our understanding of geometry but also highlighted the importance of critical thinking, visualization, and historical context in examining mathematical concepts. By embracing the complexity of geometric classification, we can develop a deeper appreciation for the beauty and intricacy of the world of shapes.

Frequently Asked Questions

1. Can a square be classified as a trapezoid?

Yes, in some mathematical contexts, a square can be classified as a special type of trapezoid because it has at least one pair of parallel sides. However, this classification is not universally accepted, as a square is more commonly recognized as a distinct quadrilateral with unique properties.

2. What are the main differences between a square and a trapezoid?

The main differences between a square and a trapezoid lie in their properties. A square has equal sides, right angles, and congruent diagonals, while a trapezoid is defined by having at least one pair of parallel sides with varying side lengths and angles.

3. Are all quadrilaterals with parallel sides considered trapezoids?

No, not all quadrilaterals with parallel sides are considered trapezoids. While trapezoids have at least one pair of parallel sides, other quadrilaterals, such as parallelograms and rectangles, also have parallel sides but differ in their additional properties.

4. How do geometric theorems help in understanding the relationship between squares and trapezoids?

Geometric theorems provide a framework for understanding the relationships between different shapes and their properties. Theorems such as the Parallel Line Theorem and the Angle-Sum Theorem offer insights into the classification of squares and trapezoids and help determine their relationships.

5. What role does visualization play in understanding geometric shapes?

Visualization is a powerful tool for understanding geometric shapes and their properties. By using diagrams, models, and interactive tools, we can better grasp the relationships between different shapes and develop a clearer understanding of geometric concepts.

6. How does the study of advanced geometric concepts relate to squares and trapezoids?

Advanced geometric concepts, such as transformations, symmetry, and topology, build upon our understanding of basic shapes like squares and trapezoids. These concepts expand our knowledge of geometric relationships and provide new insights into the classification and properties of shapes.

For further reading on geometric concepts and their applications, visit Khan Academy's Geometry Section.