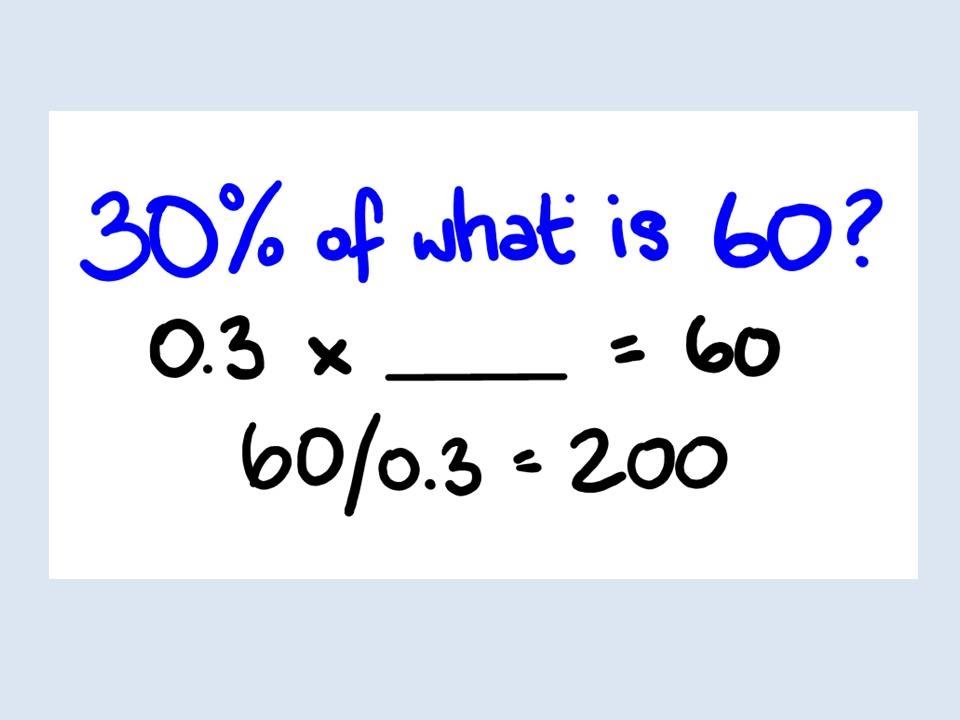Unlocking The Secrets: How To Find Percentage Of A Number

How to find percentage of a number? It’s a common question, one that echoes through classrooms, boardrooms, and households alike. Whether you're calculating a discount during a shopping spree or figuring out the interest on a savings account, understanding percentages is a crucial skill. This article aims to unravel the mysteries of percentage calculations, providing you with the tools and confidence to approach these problems with ease. By the end of this piece, the world of percentages will be as clear as day, and you'll be equipped to tackle any percentage problem that comes your way.

In the realm of mathematics and finance, percentages serve as a universal language. They represent parts of a whole, a way to express proportions and compare different values. Yet, despite their ubiquity, percentages can sometimes appear daunting or confusing. Fear not! This article is designed to demystify the process, offering step-by-step guidance on how to find percentage of a number. With practical examples and easy-to-follow instructions, you'll soon feel like a percentage pro.

So, why is it important to learn how to find percentage of a number? For starters, percentages are integral to everyday life. They help us make informed decisions, balance budgets, and understand data trends. Whether you're a student, a business professional, or simply someone keen on improving their math skills, mastering percentages is a valuable asset. This journey will equip you with the knowledge to navigate percentage problems with confidence and clarity. Let’s dive in and explore the fascinating world of percentages together!

Understanding the Concept of Percentage
The Importance of Percentage Calculations
Basic Formula for Calculating Percentage
Step-by-Step Guide: Finding Percentage of a Number
Examples of Percentage Calculations
Applications of Percentages in Daily Life
Common Mistakes in Percentage Calculations
Advanced Percentage Calculations
Using Technology for Percentage Calculations
Quick Tips for Accurate Percentage Calculations
Frequently Asked Questions
Conclusion

Understanding the Concept of Percentage

To embark on the journey of learning how to find percentage of a number, it's essential to first understand what a percentage is. A percentage is a way of expressing a number as a fraction of 100. It is denoted using the symbol "%". In essence, the term "percent" means "per hundred," which helps to standardize values, making them easier to compare.

At its core, a percentage is a dimensionless ratio or number, which allows it to be universally applicable across various fields. Whether you're dealing with statistics, economics, or simple day-to-day scenarios, percentages provide clarity and uniformity. They simplify complex data and help convey information in a more digestible format.

For instance, if you score 85 out of 100 on a test, your score can be represented as 85%. This representation quickly communicates your performance compared to the total possible score. Similarly, a 20% discount on a product signifies that you pay 80% of the original price. These examples illustrate how percentages facilitate understanding and decision-making.

The Importance of Percentage Calculations

Percentage calculations play a pivotal role in numerous aspects of life. They are not only essential in academic settings but also critical in financial planning, business analysis, and everyday shopping experiences. Understanding how to find percentage of a number empowers individuals to make informed decisions based on quantitative data.

In the financial world, percentages are indispensable. They are used to calculate interest rates, tax rates, profit margins, and investment returns. Businesses rely on percentage calculations to assess growth, performance, and risk. On a personal level, percentages help individuals manage budgets, compare prices, and evaluate savings options.

Moreover, percentages are integral to interpreting statistical data. They allow for the comparison of different datasets, making it easier to understand trends and patterns. In fields such as healthcare and education, percentages are used to track progress, measure success, and identify areas for improvement.

Basic Formula for Calculating Percentage

Calculating a percentage involves a straightforward formula. The basic formula for finding the percentage of a number is:

Percentage (%) = (Part/Whole) × 100

In this formula, "Part" refers to the portion or amount you want to calculate the percentage for, while "Whole" represents the total or entire amount. By multiplying the result by 100, you convert the fraction into a percentage.

Let's break it down with an example. Suppose you want to find out what percentage 25 is of 200. Using the formula:

Percentage = (25/200) × 100 = 12.5%

Thus, 25 is 12.5% of 200. This calculation can be applied to various scenarios, whether you're determining discounts, interest rates, or data proportions.

Step-by-Step Guide: Finding Percentage of a Number

Now that we've covered the basic formula, let's delve into a step-by-step guide on how to find percentage of a number. This guide will simplify the process, ensuring you can tackle percentage problems with confidence.

Identify the "Part" and "Whole": Determine the values representing the part and the whole in your calculation. The "Part" is the specific amount you want to find the percentage for, while the "Whole" is the total amount.
Apply the Formula: Use the formula: Percentage (%) = (Part/Whole) × 100. Substitute the identified values into the formula.
Perform the Calculation: Divide the "Part" by the "Whole" to obtain a decimal value. Multiply this result by 100 to convert it into a percentage.
Interpret the Result: The final value represents the percentage of the "Part" relative to the "Whole". This value can be used to assess proportions, compare data, or make informed decisions.

By following these steps, you'll be well-equipped to find percentages in various contexts, enhancing your numerical literacy and problem-solving skills.

Examples of Percentage Calculations

To solidify your understanding of how to find percentage of a number, let's explore some practical examples. These scenarios illustrate the versatility of percentage calculations in everyday situations.

Example 1: Calculating Discounts

Imagine you're shopping for a new pair of shoes priced at $150, and there's a 20% discount. To find the discount amount, use the formula:

Discount = (20/100) × 150 = $30

Thus, the discount amount is $30, and you'll pay $120 for the shoes.

Example 2: Determining Test Scores

Suppose you scored 45 out of 60 on a math test. To find your percentage score, apply the formula:

Percentage Score = (45/60) × 100 = 75%

Your score is 75%, indicating your performance relative to the total possible score.

Example 3: Calculating Interest

Consider a savings account with a $1,000 principal and a 5% annual interest rate. To find the interest earned in one year:

Interest = (5/100) × 1000 = $50

You earn $50 in interest over the year, demonstrating the power of percentages in financial planning.

Applications of Percentages in Daily Life

The ability to find percentage of a number is invaluable in various facets of life. Here are some common applications of percentages:

Budgeting: Percentages help allocate funds, ensuring balanced spending across different categories.
Shopping: Discounts and taxes are often expressed as percentages, aiding in price comparisons and calculations.
Health and Nutrition: Nutritional labels use percentages to indicate daily value contributions of nutrients.
Education: Test scores and grading systems frequently use percentages to evaluate performance.
Business and Finance: Profit margins, growth rates, and investment returns are calculated using percentages.

These applications highlight the significance of understanding percentage calculations in making informed decisions and enhancing numerical comprehension.

Common Mistakes in Percentage Calculations

While learning how to find percentage of a number is straightforward, there are common pitfalls to be aware of. Avoiding these mistakes will ensure accurate and reliable calculations.

One common error is confusing the "Part" and "Whole" values. It's crucial to correctly identify these components to apply the formula accurately. Another mistake is neglecting to multiply the decimal result by 100, leading to incorrect percentage values.

Additionally, overlooking units can cause confusion. Always ensure that both the "Part" and "Whole" values share the same units before performing calculations. Lastly, double-check your work to prevent arithmetic errors, especially in complex calculations involving multiple steps.

Advanced Percentage Calculations

Beyond basic percentage calculations, there are advanced techniques that expand your numerical toolkit. These methods are valuable for tackling more intricate problems and exploring deeper mathematical concepts.

Percentage Increase and Decrease

Calculating percentage increases or decreases involves determining how much a value has changed relative to its original value. The formula for percentage change is:

Percentage Change = ((New Value - Original Value) / Original Value) × 100

This formula is useful for analyzing growth, reductions, or fluctuations in data, making it applicable in finance, economics, and trend analysis.

Compound Interest

Compound interest involves calculating interest on both the initial principal and the accumulated interest from previous periods. The formula for compound interest is:

A = P(1 + r/n)^nt

Where "A" is the final amount, "P" is the principal, "r" is the annual interest rate, "n" is the number of times interest is compounded per year, and "t" is the number of years. Compound interest demonstrates the power of exponential growth and is essential for financial planning and investment strategies.

Percentage Proportions

Percentage proportions involve comparing two percentages to determine their relationship. This technique is useful for analyzing data distributions and understanding relative contributions within datasets.

Using Technology for Percentage Calculations

In the digital age, technology offers numerous tools to simplify percentage calculations. From calculators and spreadsheets to mobile apps and online resources, technology enhances accuracy and efficiency.

Calculators are readily available on smartphones, making it easy to perform quick percentage calculations on the go. Spreadsheet software, such as Microsoft Excel or Google Sheets, provides powerful functions for automating complex calculations and analyzing data trends.

Online platforms and educational websites offer interactive tools and tutorials to aid in learning and practicing percentage calculations. These resources cater to various learning styles, ensuring accessibility and support for individuals of all skill levels.

Quick Tips for Accurate Percentage Calculations

To enhance your proficiency in finding percentages, consider these quick tips for accurate calculations:

Practice Regularly: Consistent practice reinforces understanding and builds confidence in percentage calculations.
Check Your Work: Double-check calculations to catch errors and ensure accuracy.
Use Technology Wisely: Leverage calculators and spreadsheets for complex or repetitive calculations.
Understand Context: Consider the context of the problem to accurately identify the "Part" and "Whole" values.
Stay Organized: Neatly organize calculations and show all steps to track progress and identify errors.

By incorporating these tips into your mathematical routine, you'll enhance your skills and approach percentage problems with confidence and precision.

Frequently Asked Questions

1. What is the formula for finding the percentage of a number?

The formula for finding the percentage of a number is: Percentage (%) = (Part/Whole) × 100.

2. How do I calculate a percentage increase?

To calculate a percentage increase, use the formula: Percentage Increase = ((New Value - Original Value) / Original Value) × 100.

3. What are some common uses of percentages in finance?

In finance, percentages are used to calculate interest rates, tax rates, profit margins, and investment returns.

4. How can technology help with percentage calculations?

Technology offers calculators, spreadsheets, and online tools to simplify and automate percentage calculations, enhancing accuracy and efficiency.

5. What are the benefits of understanding percentage calculations?

Understanding percentage calculations aids in decision-making, financial planning, data analysis, and enhances numerical literacy.

6. How can I avoid common mistakes in percentage calculations?

To avoid common mistakes, correctly identify "Part" and "Whole" values, multiply decimals by 100, ensure consistent units, and double-check calculations.

Conclusion

In conclusion, mastering how to find percentage of a number is a valuable skill that transcends mathematical boundaries. From classrooms to boardrooms, percentages serve as a universal language, enabling individuals to make informed decisions and understand complex data. By grasping the concepts, formulas, and applications outlined in this article, you'll gain confidence and precision in tackling percentage problems.

Whether you're calculating discounts, analyzing financial data, or interpreting statistical trends, percentages offer clarity and insight. As you continue to practice and apply these skills, you'll unlock the power of percentages and enhance your numerical literacy. Embrace the journey, and let percentages empower you to navigate the world of numbers with ease and understanding.

For further exploration of percentage calculations and related mathematical concepts, consider visiting Khan Academy, a reputable educational resource offering comprehensive tutorials and practice exercises.